Highly Scalable Adaptive Mesh Refinement and its Applications

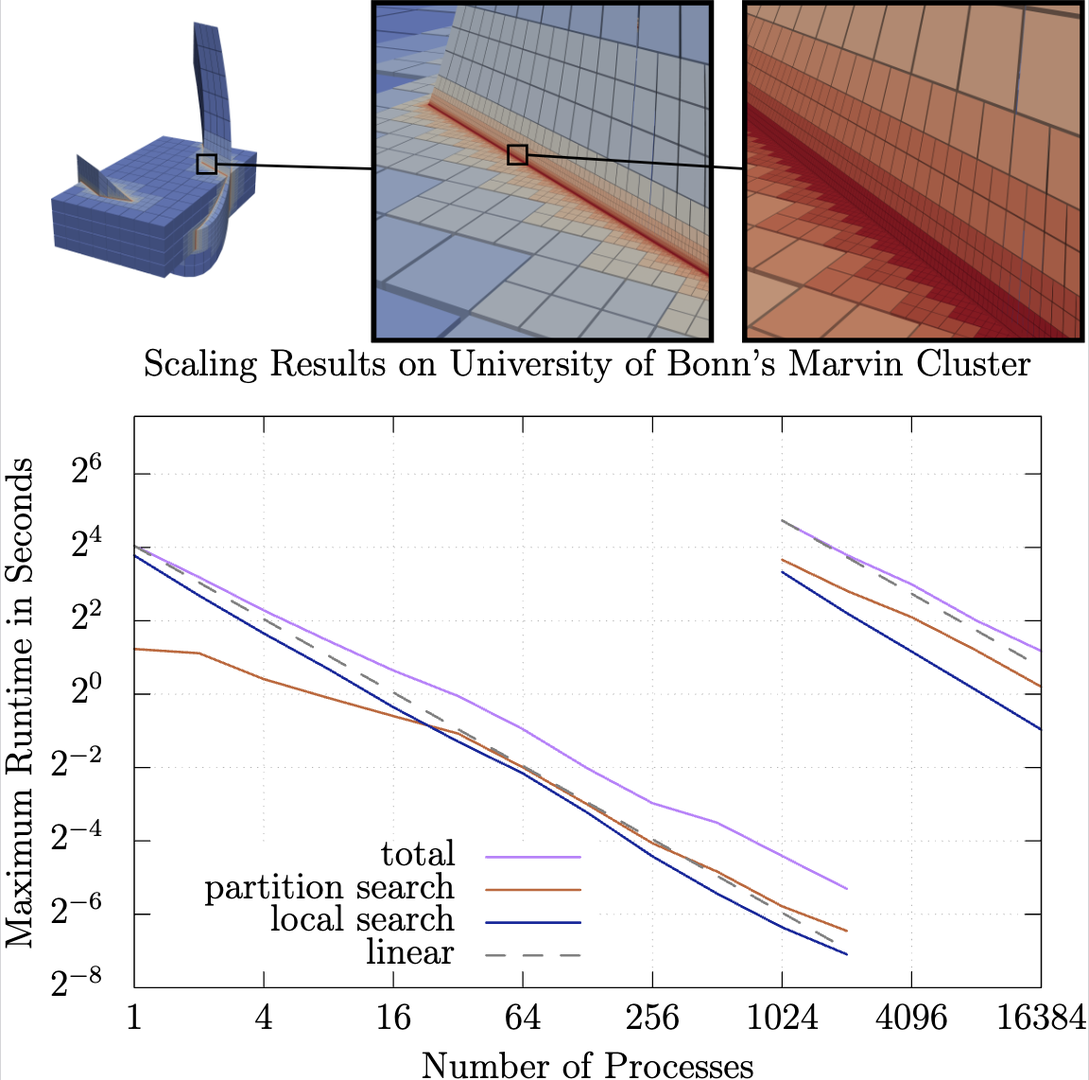
Most numerical simulation techniques rely on a mesh of computational cells that cover the domain. During a simulation it is often necessary to adapt the mesh by refining and coarsening specfic areas. Since real world simulations require enourmous amounts of mesh cells, these must be efficiently partitioned in parallel and all algorithms must operate on distributed data. The p4est software library, maintained in our research group in Bonn, provides a framework to solve essential problems of parallel adaptive mesh refinement. The central data structure is a distributed leaves-only forest of octrees. On top of that structure, we develop efficient and modular algorithms that ensure scalability to the world’s largest supercomputers. One application is the matching of multiple overlapping meshes. This challenge arises naturally in coupled or multiphysics simulations. To obtain meaningful results, the meshes have to yield a consistent solution in the overset regions. This necessitates an efficient search and exchange of solution data between several meshes of generally unrelated parallel partitions. We have developed a new overset method based on both process-local and remote searches leveraging p4est’s efficient encoding of tree traversals. We scale it successfully to 16384 MPI processes of Marvin. We will present results of generic, efficent and highly scalable new algorithms. Besides mesh overset, which is used as a builiding block in large physics simulations and sufficiently generic to apply to many other multiphysics problems, we will also show results of parallel visualization. The latter are computed using a new parallel radiosity algorithm leveraging p4est’s efficency and scalability.